The math package: Tools

Numerical tools

cutzeros

cutzeros removes trailing zeros from Maple floats: 

> fsolve(x^2-1, x);
-1.000000000, 1. 

> cutzeros(");
-1, 1

roundf

roundf rounds to a specified digit: 
> roundf(3.141592654, 4);
3.1416

slice

cuts floats. 
> slice(2.71828182845904523536028747135, 3);
2.718

cancel

deletes real and complex numbers very close to zero from an expression. 
> cancel(x + 1e-10*I + 2);
x + 2

deg & rad

Converting degrees to radians and vice versa with the convert function needs some time to input. 
> deg(Pi/4);
45 
> rad(45);
1/4 Pi

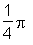
getreals

> solve(x^3-1, x);
[Maple Math]

getreals returns all real values from an expression or a sequence of expression that are real but not complex: 

> getreals(");
1

_Zval

Explicit values from the last result can be computed with _Zval: 

> _EnvAllSolutions := true:

> solve(cos(x), x);
[Maple Math] 
> _Zval(", -10 .. 10);
[Maple Math] 

> evalf(");
-7.853981635, -4.712388981, -1.570796327, 1.570796327, 4.712388981, 7.853981635

seqby

The seqby function is similar to seq but also accepts a step size. 
> seqby(x^2, x=1 .. 2, 0.25);
1.0000, 1.5625, 2.2500, 3.0625, 4.0000

recseq

conducts recursive iteration of a sequence. 
> recseq(x^2, x=0.5, 10);
.5, .25, .0625, .00390625, .00001525878906, .2328306436 10^(-9) [, ...]

Algebraic tools

convert/range

converts a RealRange expression into a Maple range: 
> convert(RealRange(0, Open(2)), range, exact);
0 .. Open(2)

convert/RealRange

convert/RealRange converts a relation or a Maple range into a RealRange expression. 
> convert({x >= 0, x < 2}, RealRange);
RealRange(0, Open(2)) 
> convert(0 .. Open(2), RR);
RealRange(0, Open(2))

getindets

getindets returns all indeterminates in an expression. 
> alias(E=exp(1)):

> getindets(Pi*x+E*y);
x, y

inter

inter determines the intersection between two intervals: 

> r1 := solve(x>-10, x);
[Maple Math] 

> r2 := solve(x<10, x);
[Maple Math] 

> inter(r1, r2);
Open(-10) .. Open(10)

rangemembers

rangemembers determines the elements included in a range. 
> rangemembers({-1, 0, 0.5, exp(1), 5, Pi}, RealRange(Open(0), Pi));
[Maple Math]

retrieve

retrieve selects those expressions from a list that contain or do not certain subexpressions: 

> t := readlib(trigsubs)(tan(x^2-1));

[Maple Math]
[Maple Math]
[Maple Math] 

> retrieve(t, [sin, cos, x^2-1]);
[Maple Math]

un

un is an abbreviated unapply function. 
> f1 := un(diff(x^2-x, x));

back

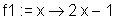
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mplmtool.htm