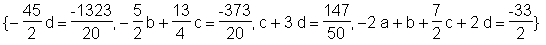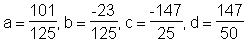

mat
This function facilitates defining matrices. Instead of a list of (many) lists just pass a string of all the components separated by spaces. Rows are separated by a semicolon (or one of three other special characters).
> A := mat(`1 a 3; 4 Pi 6; 8 9 sqrt(10)`);
![A := MATRIX([[1, a, 3], [4, Pi, 6], [8, 9, 10^(1/2)]])](maplev/math/mathou28.gif)

redefdim
allows to redefine the dimensions of a matrix or array.
> redefdim(A, 1 .. 2, 1 .. 2);
![MATRIX([[1, a], [4, Pi]])](maplev/math/mathou29.gif)

V and print/vector
The function math/V now also accepts strings and now is fully compatible with the linalg package:
> v := V(`1 2 3`);
v := [1, 2, 3]
To display vectors vertically, use the vecvert switch (you do not need to use V to define vectors, you may also use array or vector).
> vecvert;
vertical
> eval(v);
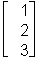 To change back to horizontal display, type
To change back to horizontal display, type
> vechori;
horizontal
> eval(v);
[1, 2, 3]

reduce
Gaussian elemination of a system of linear equations.
> sys := {
> a-3*b+3/2*c-d=-104/10,
> -2*a+b+7/2*c+2*d=-165/10,
> a-2*b+12/10*c+2*d=0,
> 3*a+b-c-3*d=-7/10};
> reduce(sys, p);
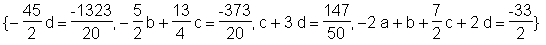
> p;
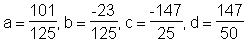

isDependent
checks whether column vectors are dependent.
> isDependent(mat(`-2 3 -4 -2; 3 1 1 1, -4 -5 2 0`));
true

Matrix types
math/isDiagonal, math/isIdentity, math/isSymmetric, math/isAntiSymmetric, and math/isQuadratic check whether a matrix is of a specific type.
> isSymmetric(mat(`a b; b c`));
true


Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mplmla.htm
![A := MATRIX([[1, a, 3], [4, Pi, 6], [8, 9, 10^(1/2)]])](maplev/math/mathou28.gif)