Maple V bilingual - The math package: Analysis

The math package primarily is a supplement to the student package shipped with Maple V and features a lot of functions which are not included in the latter package.

> restart: libname := `c:/maplev4/math`, libname: 

> with(math);

[END, Makehelp, PSconv, V, Write, WriteLn, _Zval, addlib, addtbl,
    arclen, assumed, asym, cartgridR3, cartprod, cont, curvature,
    curveplot, cutzeros, deg, dellib, deltbl, domain, entry, extrema,
    fnull, getindets, getreals, gridplot, inflection, inter, isCont,
    isDiff, liblist, lineangle, load, ls, mat, mean, mreadlib,
    nondiff, normale, rad, rangemembers, redefdim, retrieve, rootof,
    rotation, seqplot, setdef, singularity, slopefn, symmetry,
    tangente, un]

fnull

solve and fsolve do not properly work with (inverse) transcendental functions:

> fsolve(sin(x), x=-10 .. 10);

3.141592654

                                     
> fnull(sin(x), x=-10 .. 10);

-9.424777961, -6.283185307, -3.141592654, 0, 3.141592654, 6.283185307, 9.424777961

(However, you may set the global variable _EnvAllSolutions := true so that solve returns general solution(s).)

extrema and inflection

The functions math/extrema and math/inflection find extrema and inflection points of a function in one real on a given interval. Especially math/extrema is intended to replace the student/extrema functions.

> extrema(x^5-x^3, x=-10 .. 10);

$1/5*15^(1/2), -1/5*15^(1/2)$

> extrema(x^5-x^3, x=-10 .. 10, floats);

-.7745966692, .7745966692

                     
> extrema(x^2, x=-10 .. 10, max); # no result

> extrema(x^2, x=-10 .. 10, min);

> extrema(x^3, x=-10 .. 10); # no result

> inflection(x^3, x=-10 .. 10);

> inflection(x^2*sin(x), x=-10 .. 10, eps=1e-5);

-9.819003402, -6.832145747, -3.994444716, -1.519855298, 0,
1.519855299, 3.994444716, 6.832145747, 9.819003402

cont

cont checks whether a function in one real is continuous about a point.

> cont((x^2-3*x+2)/(x^2+2*x-3), x=1);

$false, undefined, removable = -1/4$

singularity

singularity determines discontinuities and checks them for correctness (as opposed to discont):

> readlib(discont)(sqrt(x), x);

{0}

> singularity(sqrt(x), x);

{ }

> singularity(tan(x), x);

$[Maple Math]$

pole, jump, removable

Poles, jump and removable discontinuities are determined by pole, jump, and removalble:

> pole(1/x, x);

{0}

> removable(sin(x)/x, x);

{0}

> jump(floor(x), x);

{8, -9, 9, -10, 5, -6, 6, -7, 7, -8, -3, 3, -4, 4, -5, -1, 1, -2, 2, 0, 10}

cartprod

provides an interface to combinat/cartprod and returns a sequence of pairs instead of a table that has to be evaluated by the user.

> cartprod([[1, 2, 3, 4], [x, y, z]], 'p');

[1, x],
[1, y],
[1, z],
[2, x],
[2, y],
[2, z],
[3, x],
[3, y],
[3, z],
[4, x],
[4, y],
[4, z]

> p;

[1, x], [1, y], [1, z], [2, x], [2, y], [2, z], [3, x], [3, y], [3, z], [4, x], [4, y], [4, z]

gridplot, asym, un

gridplot plots graphs of functions like plot, but adds 'graph paper' to the drawing.

> f := x -> (1/2*x^3-3/2*x+1)/(x^2+3*x+2);

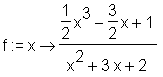
$f := proc (x) options operator, arrow; (1/2*x^3-3/2*x+1)/(x^2+3*x+2) end$

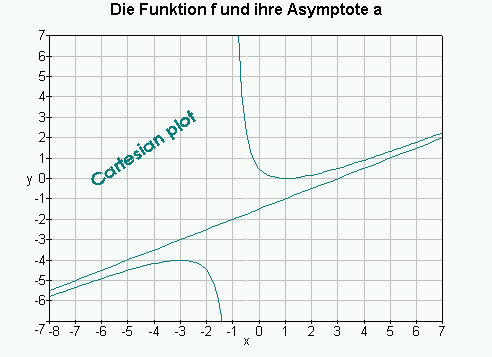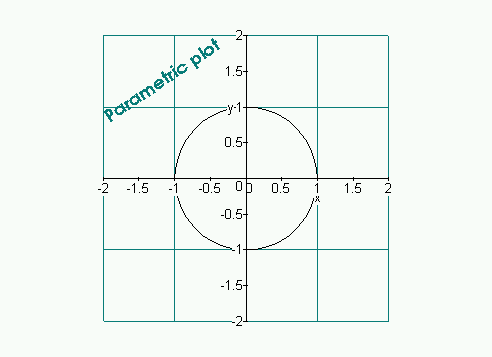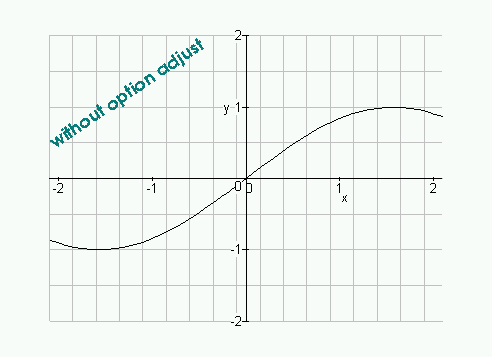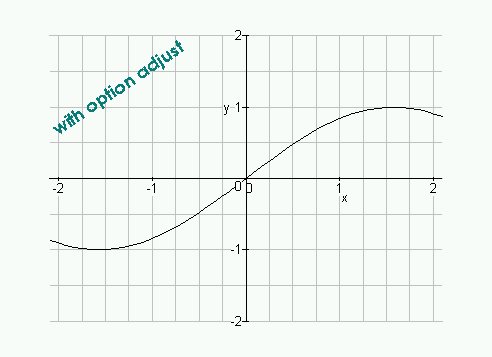
First let us determine the oblique asymptote with function math/asym:

> asym(f(x));

$1/2 x - 3/2$

Use un for an abbreviated version of unapply:

> a := un(");

$a := x -> 1/2 x - 3/2$

Besides accepting all valid plotoptions, gridplot has two additional options:

units: specifies the intervals a tickmark is plotted
gridcolor: specifies another Maple color for the grid (dafault is gray).

> gridplot({f(x), a(x)}, x=-8 .. 7, y=-7 .. 7,
>    discont=true,
>    axes=box, 
>    labels=[`x`, `y`],
>    units=1,
>    color=darkcyan,
>    axesfont=[HELVETICA, 10],
>    titlefont=[HELVETICA, BOLD, 12],
>    title=`Die Funktion f und ihre Asymptote a`);

You may also pass parametric functions to gridplot. math includes a new color 'darkcyan'. See ?math, init for more colors.

> gridplot([sin(t), cos(t), t=-Pi .. Pi], x=-2 .. 2, y=-2 .. 2, 
>    gridcolor=darkcyan, 
>    units=0.5,
>    scaling=constrained);

You specify the adjust option to move the grid left or right and up or down.

> gridplot(sin(x), x=-2.1 .. 2.1, y=-2 .. 2, 
>    units=1, step=[0.25, 0.5]);

> gridplot(sin(x), x=-2.1 .. 2.1, y=-2 .. 2, 
>    units=1, step=[0.25, 0.5], adjust=[0.1, 0]);

symmetry

Determining the kind of symmetry of a function in one real is tedious with type/evenfunc and type/oddfunc, so use symmetry:

> symmetry(x^2);

true, even

> symmetry(x^3-x);

true, odd

> symmetry(exp(x));

false, neither even nor odd

PSconv

convergence of power series:

> s := Sum((-1)^(n+1)*(x-1)^n/n, n=1 .. infinity);

Radius of convergence of series s:

> PSconv(s);

1 More details:

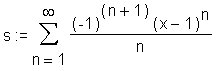
> PSconv(s, limit);

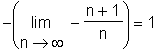
Evaluate the range of convergence and evaluate its boundary points:

> PSconv(s, range);

RealRange(Open(0), 2)

tangente, normale and curveplot

Let f be a function in one real x:

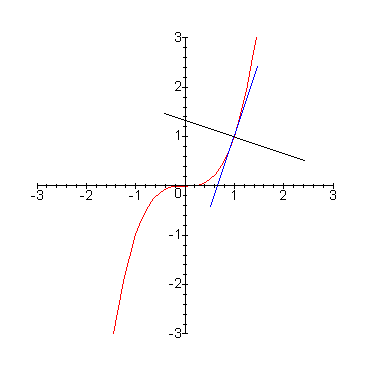
> f := x -> x^3:

Determine the tangent and normal lines at the point x=1:

> tangente(f(x), x=1);

3 x - 2

> normale(f(x), x=1);

Plot the graph of f along with the tangent and normal lines:

> curveplot(f(x), x=1, [normalline, tangentline], 
>    x=-3 .. 3, y=-3 .. 3, tangentcolor=blue, scaling=constrained, 
>    length=3, normalcolor=black);

arclen

arc lengths of both explicit or parametric functions on [a, b]:

> assume(r, positive):

> 4*arclen(sqrt(r^2-x^2), x=0 .. r);

> arclen([t, t^2, 2/3*t^3], t=0 .. 3);

mean

Determine linear and quadratic means:

> mean(sin(x), x=0 .. Pi, linear);

> mean(sin(x), x=0 .. Pi, quadratic);

curvature

evaluates the curvature of a real-valued function:

> curvature(sin(x+t), x);

slopefn

slopes of functions in x at a point a can also be determined:

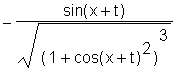
> slopefn(x^2, x=t);

2 t

lineangle

The angle of intersection between two curves can be computed easily:

> lineangle([2*x-3, 1/2*x+1]);

convert/explicit

Parametric functions can be converted into their explicit forms with convert/explicit:

> convert([1/2*t^2+2, 3/4*t^2+1], explicit);

rotation

The new function math/rotation evaluates characteristics of bodies of rotation:

> assume(r, positive):

> rotation(sqrt(r^2-x^2), x=0 .. r, area, xaxis);

> rotation(sqrt(x), x=0 .. 4, area, yaxis);

> rotation(x^2, x=0 .. sqrt(2), vol, yaxis);

> rotation(x*exp(-x), x=0 .. 1, vol, xaxis, float);

.2539377490

> rotation(sqrt(4-x), x=0 .. 4, xaxis, center);

> rotation((4-x)*sqrt(2*x), x=0 .. 4, xaxis, moment, float);

domain

Function domain determines the domain of a function in one real:

> f := x -> sqrt(x^3+4*x^2+4*x);

$[Maple Math]$

> domain(f(x));

$[Maple Math]$

isCont and isDiff

isCont (an interface to cont) and isDiff determine whether a function is continuous and differentiable, respectively, at a given point.

> isCont(abs(x), x=0);

true

> isDiff(abs(x), x=0);

false

nondiff

nondiff determines all those points at which a function is not differentiable:

> nondiff(arcsin(2*abs(x)*sqrt(1-x^2)), x);

$[Maple Math]$

END

END determines extrema at points where a function is not differentiable (extrema currently does not return results in this case):

> extrema(abs(x), x);

> END(abs(x), x);

Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mplmana.htm