|
Kapitel Vier: Analysis |
 |
|
|
|
Kapitel 3
|
|
Kapitel Vier: Analysis |
 |
|
|
|
Kapitel 3
|
Definiert sei eine Funktion f(x) = 1/x, die wir mit limit auf ihren Grenzwert (limit) im Unendlichen (infinity) untersuchen. Dem Befehl wird die Funktion und die interessierende Stelle, an der nach dem Grenzwert gesucht werden soll, übergeben. Für das Verhalten im Unendlichen steht die Konstante infinity zur Verfügung.
> restart: > f := x -> 1/x: > limit(f(x), x=+infinity);
> limit(f(x), x=-infinity);
Nun erfolgt die Untersuchung der Funktion f an der Stelle x=0:
> limit(f(x), x=0);
> f(0); Error, (in f) division by zero
Links- und rechtsseitiger Grenzwert:
> Limit(f(x), x=0, left) = limit(f(x), x=0, left);
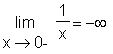
> Limit(f(x), x=0, right) = limit(f(x), x=0, right);
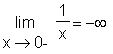
Zusätzlich zu den Parametern Funktion und Stelle wird limit jetzt auch mitgeteilt, von welcher Seite aus der Grenzwert berechnet werden soll: von links (left) oder von rechts (right). Der Befehl Limit ist ein sogenanntes träges (inert) Kommando: Es bewirkt nicht die Errechnung, sondern dient nur der Anzeige unberechneter Formeln. Mit value können Sie eine Berechnung des trägen Ausdruckes erzwingen. Weitere träge Befehle finden sich im Kapitel 7.
Die Stetigkeit (continuity) überprüfen Sie mit iscont. Dieser Befehl muß vorher erst durch den Aufruf readlib(iscont) aktiviert und das zu untersuchende Intervall angegeben werden. Als optionalen dritten Parameter können Sie 'closed' (mit den Apostrophen) übergeben, dann wird das Intervall inklusive dessen Grenzen untersucht.
> readlib(iscont): > iscont(f(x), x=-1 .. 1);
false steht für die Unstetigkeit der Funktion im gegebenen Intervall, true für die Stetigkeit. Die Funktion f(x) = 1/x ist im Intervall [-1, +1] nicht stetig.
> restart: > g := x -> 1/10*x^3-x;
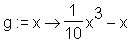
> readlib(iscont): > iscont(g(x), x=-4 .. 4);
> restart: > folge := (-1)^n+1/n;
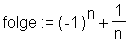
Mit seq werden die ersten 10 Glieder der Folge (sequence) berechnet und der Variable a zugewiesen. Als zweites Argument wird der Laufbereich index=m .. n angegeben:
> a := seq(folge, n=1 .. 10);
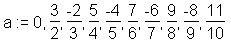
Auf alle Glieder können Sie durch Angabe ihres Indexes zugreifen:
> a[1], a[2], a[3];oder
> a[1 .. 3];
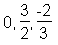
Jetzt wird eine Teilmenge an als sog. Liste (list) konstruiert, in die das dritte, fünfte und siebte Folgeglied abgespeichert wird:
> an := [a[3], a[5], a[7]];
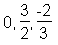
Listen sind in Maple sehr leistungsfähig.
Die in seq benutzte Laufvariable n hat jetzt einen um 1 höheren Wert als der Index des letzten Folgegliedes von a:
> n;
Der Indexbereich kann bei seq natürlich beliebig vorgegeben werden.
> n := 'n': > folge := n/(n+1);
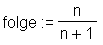
> seq(folge, n= 3 .. 7);
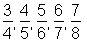
> n:='n':
Grenzwerte von Folgen:
> Limit(folge, n=0) = limit(folge, n=0);
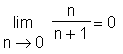
> Limit(folge, n=infinity) = limit(folge, n=infinity);
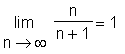
Die ersten zwanzig Glieder der Folge werden zusammen mit ihrem jeweiligen Index jetzt als Liste der Variable pts zugewiesen, diese dient der graphischen Anzeige der Folge.
> pts := [seq([n, folge(n)], n=1 .. 20)];
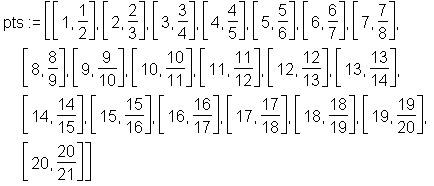
> gr1 := plot({pts}, x=1..20, y=0.5 .. 1.1, style=point):
> gr2 := plot(1, x=1..20, y=0.5 .. 1.1, style=line):
> with(plots):
> display({gr1, gr2});
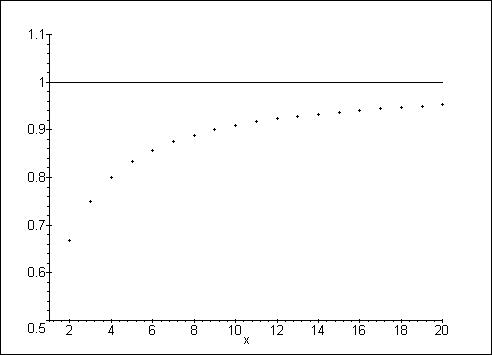
Die nächste Folge hat keinen Grenzwert, dafür aber Häufungspunkte. Jene werden von Maple in der Form a .. b ausgegeben, will heißen: im abgeschlossenen Intervall [a, b]. Dies muß aber nicht bedeuten, daß im Intervall nur Häufungspunkte liegen. Daher sollte auf jedem Fall der Graph der Folge zur weiteren Analyse angezeigt werden.
> restart: > a := n-> (-1)^n*n/(n+2);
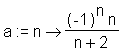
> Limit(a(n), n=infinity) = limit(a(n), n=infinity);
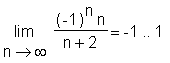
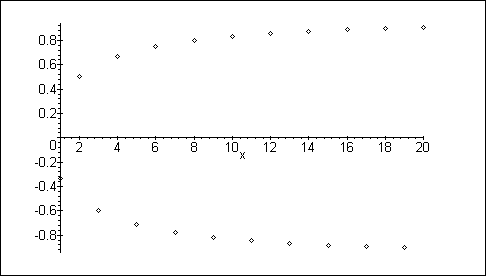
Diese Folge besitzt nur die Häufungspunkte -1 und +1.
Ist eine Folge bestimmt divergent, d.h. sie strebt entweder gegen den uneigentlichen Grenzwert -unendlich oder gegen +unendlich, so meldet Maple '-infinity' bzw. 'infinity'.
> Limit(n^2, n=infinity) = limit(n^2, n=infinity);
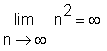
> Limit(-n^2, n=infinity) = limit(-n^2, n=infinity);
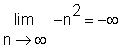
Ist eine Folge unbeschränkt aber nicht bestimmt divergent, so liefert Maple das Resultat 'undefined':
> Limit(((-1)^n+1)*n, n=infinity) = limit(((-1)^n+1)*n, n=infinity);
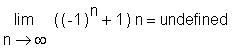
Ein etwas anderer Einsatz von seq: Berechnung der ersten vier Ableitungen von 'ln(x)'.
> seq(diff(ln(x), x$n), n=1 .. 4);
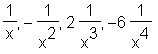
> n := 'n':
Summen lassen sich mit sum berechnen, der erste Paramter ist die Folge, der zweite der Laufbereich n von a bis b (n=a .. b); dieselbe Syntax gilt für Produkte.
> folge1 := (-1)^n*1/n;
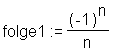
> Sum(folge1, n=1 .. 10)=sum(folge1, n=1 .. 10);
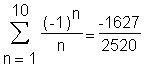
> sum(folge1, n=1 .. infinity);
> folge2 := 2*n+1;
> Product(folge2, n=1 .. 10) = product(folge2, n=1 .. 10);
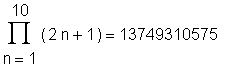
> product(folge2, n=5 .. 7);
> 5!;
oder statt n!:
> factorial(5);
Der Binomialkoeffizient n über k:
> binomial(n, k);
> binomial(4, 2);
1) (func1@func2)(var)
2) func1(func2(var))
> restart: > f := x -> exp(2*x);
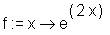
> g := x -> 2*x-7;
> `(f@g)(x)`=(f@g)(x);
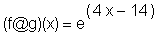
> f(g(x));
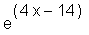
Mit diff können Sie die Ableitungen einer Funktion berechnen. Das erste Argument von diff ist die abzuleitende Funktion, das zweite die Variable, nach der abgeleitet werden soll. Dabei kann mit $n die n-te Ableitung angegeben werden. Die resultierende Ableitungsterme werden mit unapply den Funktionen f1, f2 und f3 zugewiesen.
> restart: > f := x -> -x^3+3*x+4;
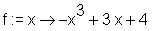
> f1 := unapply(diff(f(x), x), x);
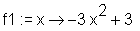
> f2 := unapply(diff(f(x), x$2), x);
> f3 := unapply(diff(f(x), x$3), x);
Die Graphen:
> pf0 := plot(f(x), x=-3 .. 3, linestyle=1, color=navy):
> t0 := textplot([1.6, f(1.6), `f(x)`], color=navy,
> align={ABOVE, RIGHT}):
> pf1 := plot(f1(x), x=-3 .. 3, linestyle=2, color=black):
> t1 := textplot([-2.6, f1(-2.6), `f'(x)`], color=black,
> align={BELOW, RIGHT}):
> pf2 := plot(f2(x), x=-3 .. 3, linestyle=5, color=red):
> t2 := textplot([-1.5, f2(-1.5), `f''(x)`], color=red,
> align={ABOVE, RIGHT}):
> pf3 := plot(f3(x), x=-3 .. 3, linestyle=4, color=magenta):
> t3 := textplot([-1, f3(-1), `f'''(x)`], color=magenta,
> align={BELOW}):
> with(plots):
> display({pf0, t0, pf1, t1, pf2, t2, pf3, t3},
> scaling=unconstrained);
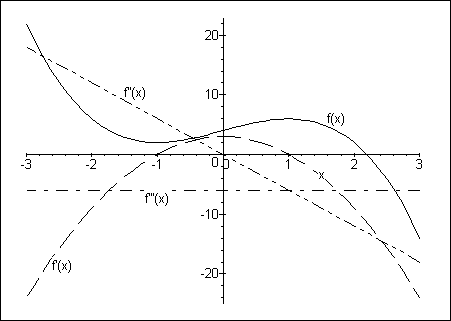
Die Extremwerte (extreme values): f '(x)=0;
> solve(f1(x)=0, x);
f ''(x) <> 0;
> f2(-1);
> f(-1);
f ''(-1) = 6 > 0 -> lok. Minimum (local minimum) bei x=-1; T(-1, 2)
> f2(1);
> f(1);
f ''(1) = -6 < 0 -> lok. Maximum (local maximum) bei x=1; H(1, 6)
Die Wendepunkte (inflection points): f ''(x) = 0;
> solve(f2(x)=0, x);
f'''(x) <> 0;
> f3(0);
> f(0);
f '''(0) = -6 <> 0 -> Wendestelle bei x=0; W(0, 4)
Eine andere Möglichkeit der Extremwertberechnung existiert mit minimize und maximize aus dem Paket 'student'. Diese beiden Befehle berechnen allerdings nur die Ordinatenwerte der Extremstellen.
Hinweis: Sowohl in Release 3 als auch Release 4 sind die Funktionen student/extrema, student/maximize und student/minimize fehlerhaft (in Release 4 bei trigonometrischen Ausdrücken). Als Ersatz lassen sich u.a. die Funktionen des Paketes math verwenden (math/ex, math/inflection).
> with(student): > minimize(f(x));
> maximize(f(x));
Natürlich können Sie mit solve die zugehörigen Abszissenwerte berechnen, nur werden dabei auch die x-Werte von Nicht-Extremstellen angezeigt, so daß man zur schnellen Identifizierung den Graphen der Funktion aufrufen muß. Zudem wird in diesem Beispiel jeweils eine Lösung doppelt angezeigt.
> solve(2=f(x), x);
> solve(6=f(x), x);
Der sog. Differentiationsoperator D kombiniert die Berechnung der Ableitungen von Funktionen mit einer Funktionszuweisung und ist somit eine Verkürzung bzw. einfacher in der Handhabung als diff gefolgt von unapply. Die Funktion wird in der Pfeilschreibweise definiert. Dem Operator D wird nur der Funktionsname in Klammern übergeben.
> restart: > f := x -> x^3: > f1 := D(f);
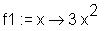
> f1(2);
Setzt man bei D hinter den Funktionsnamen das Argument der Funktion in Klammern, so wird ein unapply nicht durchgeführt. Dieses ist dann äquivalent zu der bekannten Anwendung des Befehles diff.
> D(f)(x) = diff(f(x), x);
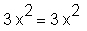
Zur Berechnung der n-ten Ableitung einer Funktion stellen Sie hinter D den Wiederholungsoperator @@, gefolgt von der Angabe der gewünschten Ableitung. Die entstandene Zeichenfolge wird von Klammern eingeschlossen.
> f2 := (D@@2)(f);
Zur Berechnung der partiellen Ableitung einer Funktion zweier Veränderlicher wie
> f := (x, y) -> -4*x^3*y^2+3*x*y^4-3*x+2*y+5;
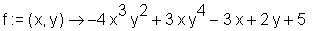
übergibt man dem Befehl diff als zweiten Parameter diejenige Variable, nach der differenziert werden soll - die jeweils andere Veränderliche wird dann als Konstante aufgefaßt.
> diff(f(x, y), x);
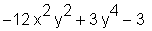
> f1x := unapply(%, x, y);
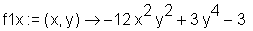
> f1y := unapply(diff(f(x, y), y), x, y);
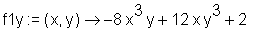
> f1x(1, 2);
> f1y(1, 2);
Die n-te Ableitung wird wie bei Funktionen mit nur einer Unbekannten ermittelt, hier für n=3:
> diff(f(x, y), x$3);
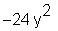
Auch bei partiellen Ableitungen erspart der Differentiationsoperator D Tipparbeit. Die Angabe der zu differenzierenden Variablen erfolgt nicht durch Nennung jener Unbekannten (z.B. 'x'), also der alphanumerischen Zeichenfolge, sondern durch Angabe des (numerischen) i-ten Argumentes der partiell zu differenzierenden Funktion in eckigen Klammern.
> restart: > f := (x, y) -> x^3*y^3:Differentiation nach 'x':
> f1x := D[1](f);
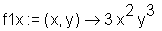
Differentiation nach 'y':
> f1y := D[2](f);
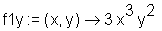
Die Berechnung der n-ten partiellen Ableitung geschieht (abweichend von Funktionen mit einer Unbekannten) durch n-malige Anwendung des Differentiationsoperators.
> f2x := (D@@2)[1](f);
syntax error:
f2x := (D@@2)[1](f);
^
> f2x := D[1](D[1](f));
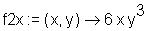
Gegeben sei eine Funktion f mit einer Unabhängigen x.
> restart: > f := x -> x^3-sin(x)+ln(x);
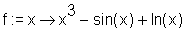
Das unbestimmtes Integral (indefinite integral) berechnen Sie mit dem Befehl int, wobei als erstes Argument die zu integierende Funktion und als zweites Argument die unabhängige Variable genannt wird.
> int(f(x), x);
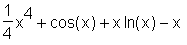
Bei bestimmten Integralen (definite integral) gibt man die Grenzen mit dem Zusatz x=untere_Grenze .. obere_Grenze an, z.B.:
> int(1/3*x^3+2*x^2-x, x=0 .. 2);
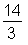
Achten Sie bei der der bestimmten Integration auf den Wertebereich der Integralfunktion.
> f := x -> sin(x): > int(f(x), x=-Pi/2 .. Pi/2);
Verwenden Sie daher für Flächenberechnungen die Absolutfunktion: R3 gibt ein unausgewertetes Integral zurück, welches mit evalf numerisch bestimmt werden kann. R4 ermittelt sofort - ohne Umweg über evalf - die Lösung.
> int(abs(f(x)), x=-Pi/2 .. Pi/2);
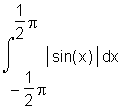
> evalf(%);
Existieren mehrere Nullstellen, so kann die Eingabezeile sehr lang werden. Es empfiehlt sich, die Nullstellen in einer Liste abzuspeichern. Danach kann der Befehl sum auf diese Liste zugreifen. nops gibt die Anzahl der in der Liste befindlichen Einträge an. Damit der Indexbereich der Liste durch den Zugriff N[n+1] nicht überschritten wird (dieses würde zu einem Syntaxfehler führen), muß zur Festlegung der rechten Grenze von n der Wert 1 von nops(N) abgezogen werden.
> N := [-Pi/2, 0, Pi/2];
> sum(abs(int(f(x), x=N[n] .. N[n+1])), n=1 .. nops(N)-1);
> n := 'n':Integration durch Substitution: Zunächst wird der träge Integrationsbefehl Int (mit großem Buchstaben i) eingesetzt und der unausgewertete Ausdruck einer Variablen zugewiesen.
> restart: with(student): > i1 := Int(2*x*sin(x^2+1), x);
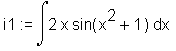
> changevar(x^2+1 = z, i1, z);
Das Integral wird nun ermittelt, bei trägen Kommandos bzw. Ausdrücken erzwingt value die Berechnung:
> value(%);
Resubstitution:
> changevar(z=x^2+1, %, x^2+1);
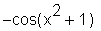
oder via
> subs(z=x^2+1, %%);
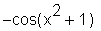
Partielle Integration:
> restart: > with(student): > intparts(Int(x*exp(x), x), x);
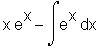
> evalf(Int(exp(x), x=1 .. 2));
Bemerkung: Bei unbestimmten Integralen fehlt bei der Berechnung grundsätzlich die Integrationskonstante 'c'.
Der Befehl series entwickelt entweder Taylor-, Laurent- oder allgemeine Potenzreihen, je nach Typ des übergebenen Ausdruckes; der Entwicklungspunkt wird als zweiter Parameter dem Kommando mitgeteilt:
> series(sin(x), x=0);
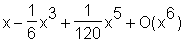
Ein optionaler dritter Parameter legt die maximale Ordnung fest, der Vorgabewert ist 6:
> series(sin(x), x=0, 10);
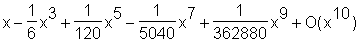
Den Vorgabewert können Sie auch allgemein durch Änderung der Systemvariable Order bestimmen:
> Order := 7;
> reihe0 := unapply(series(sin(x), x=0), x);
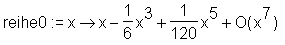
Es fällt auf, daß die Reihenentwicklung jedes Mal mit dem Ordnungsterm O(...) endet, dabei ist O der Buchstabe O.
> plot(reihe0(x), x=-4 .. 4); Warning in iris-plot: empty plot > reihe0(3); Error, (in reihe0) invalid substitution in seriesMit dieser Ausgabe lassen sich so oftmals keine weiteren Berechnungen durchführen, man muß den Term O(...) eliminieren; dies geschieht am sichersten mit subs, indem Sie den Ordnungsterm O() gleich Null setzen:
> reihe1 := unapply(series(sin(x), x=0), x);
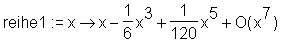
> reihe2 := unapply(subs(O(1)=0, reihe1(x)), x);
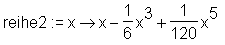
> plot({reihe2(x), sin(x)}, x=-4 .. 4, scaling=constrained);
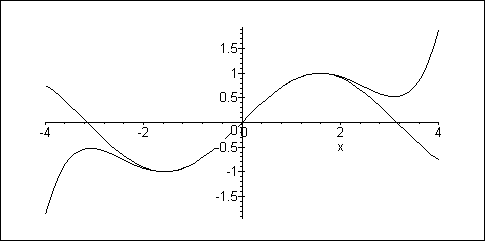
Taucht das Argument nicht in dessen Wurzelschreibweise auf, so kann der Ordnungsterm auch eleganter und einfacher mit convert/polynom umgeformt werden:
> reihe3 := convert(series(cos(x), x=Pi), polynom);
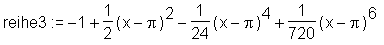
Gegenbeispiel:
> reihe4 := convert(series(sqrt(tan(x)), x=0), polynom);
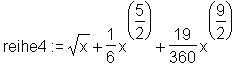
Die Angabe der Reihenentwicklung als Summenformel erfolgt mit FPS aus der Share Library. Weitere Informationen zu dieser sind in Kapitel 7 enthalten. Der zweite Parameter von FPS gibt den Entwicklungspunkt an.
> with(share); See ?share and ?share,contents for information about the share library
In Release 3 laden Sie FPS mit readshare aus der Kathegorie calculus. Release 4-Nutzer geben statt calculus den Namen analysis an.
> readshare(FPS, analysis);
Release 5 wartet mit einem vereinfachten Share-Initiallisationsverfahren auf. Auch hier muß Share mit with(share) aktiviert werden, die einzelnen zu ladenden Funktionen oder Pakete widerum mit with, wobei die Angabe der Kathegorie wegfällt.
> with(FPS): Share Library: FPS Author: Gruntz, Dominik. Description: FPS function attempts to find [...] > FPS(sin(x), x=0);
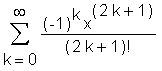
> FPS(1/x, x=1);
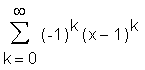
Abschnittweise definierte Funktionen können Sie mit der Anweisung piecewise realisieren. Das Kommando steht in Release 5 sofort zur Verfügung, muß aber in Release 3 und 4 zuvor mit
> readlib(piecewise):aktiviert werden.
Beachten Sie, daß die Ergebnisse dieses Befehles mit Vorsicht zu genießen sind, wie gleich demonstriert wird.
Angenommen Sie möchten eine Funktion S mit folgenden Bereichen definieren:
Für jeden Abschnitt werden in piecewise zwei Argumente eingesetzt: das erste für den Definitionsbereich in Form einer Relationsbedingung, das zweite für den Funktionsterm; dieses können Sie beliebig oft wiederholen. Erfüllt kein Argument eine der vom Benutzer vorgegebenen piecewise-Bedingungen, so gibt die Funktion vorgabemäßig den Wert 0 zurück (in Release 3 hingegen den Wert undefined); Sie können allerdings einen anderen, beliebigen Wert als letztes Argument angeben.
Die Bedingung kann alle mathematischen Vergleichsoperationen enthalten: <, <=, = , >, >=. Die Verwendung von Booleschen Operatoren and, or und not ist im Gegensatz zu den Vorgängerversionen in Release 5 zugelassen.
> S := x -> piecewise( > x < 0, -x^3, x < Pi/2, 1, x >= Pi/2, sin(x));
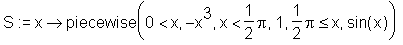
Einige Anwendungen:
> for x from -2 to 2 do > lprint(x, S(x)) > od; -2 8 -1 1 0 1 1 1 2 sin(2) > x := 'x':S ist an der Stelle x=0 unstetig, daher gibt man zur Berechnung des Grenzwertes an dieser Stelle bei limit an, von welcher Seite Maple sich der Stelle nähern soll.
> limit(S(x), x=0, left);
> limit(S(x), x=0, right);
Differenzieren können Sie ebenfalls:
> s := unapply(diff(S(x), x), x);
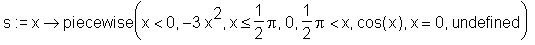
> s(0), s(Pi/2);
Bei dem Funktionsaufruf s(0) gibt Release 5 den Wert 0 zurück, obschon - wie oben ersichtlich - die Ableitung an der Stelle 0 nicht existiert. piecewise durchläuft die ihm übergebenen Bedingungen von links nach rechts. Da 0 <= Pi/2, gibt die Funktion den Wert 0 zurück. Die Bedingung x = 0, undefined wird ignoriert.
Der Graph der Funktion S und deren Ableitung:
> with(plots):
> plS := plot(S(x), x=-1 .. 4, y=-2 .. 2):
> txS := textplot([2.8, S(2.8)+0.3, `S(x)`], align={above, right}):
> pls := plot(s(x), x=-1 .. 4, y=-2 .. 2, linestyle=4, color=navy):
> txs := textplot([2, s(2)-0.2, `s(x)`], align={below, left}):
>
> display({plS, txS, pls, txs}, axes=frame);
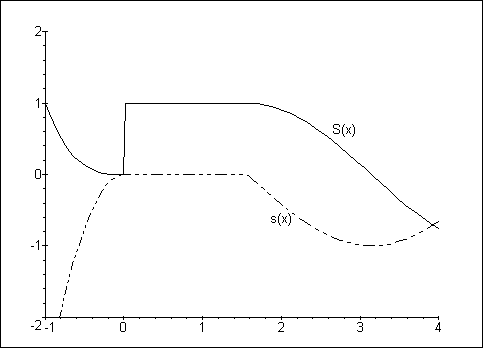
In Release 3 ist die Integration von piecewise-Funktionen nicht möglich. In Release 4/5 weist piecewise deutliche Verbesserungen und Erweiterungen auf: Die Ausgabe ist sehr übersichtlich geworden, die Ergebnisse sind meist genauer und auch Integrationen können Sie vornehmen:
> diff(S(x), x);
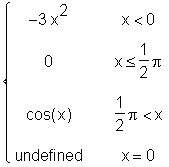
> int(S(x), x);
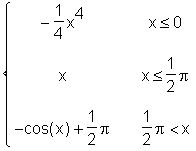
Im Gegensatz zu int im allgemeinen bzw. den anderen Spalten der obigen Ausgabe wird eine genau spezifizierte Integrationskonstante (1/2*Pi) angegeben.
Wenn die Funktion in einem bestimmten Bereich undefiniert bleiben soll, so wird der 'Wert' undefined benutzt:
> k := x -> piecewise(x < 0, -1, x = 0, 0, x < 2, undefined, > x >= 2, 1);
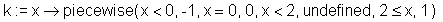
> k(-1), k(0), k(1), k(2);
Der Bereich des letzten Abschnittes braucht nicht angegeben zu werden, es genügt allein die Angabe des Funktionstermes:
> l := x -> piecewise(x < 0, -1, 1);
> l(0);
Bei der Angabe der Intervalle sollten Sie grundsätzlich bis auf den letzten Abschnitt mit <=, < oder = arbeiten. Geben Sie 'mittendrin' eine >= oder >-Relation an, so führt dies zu falschen Ergebnissen, da bei einem Wert, der eine Bedingung erfüllt, die nachfolgenden Bedingungen nicht mehr geprüft werden (s.o.).
> f := x -> piecewise(x < 0, -x^3, x >= 0, 1, x >= Pi/2, exp(x)):
^
|
> f(2);
Die Stelle x=2 fällt in den Wertebereich von sin(x), daher hätte der Funktionswert exp(2) zurückgegeben werden müssen.
Allgemeine Darstellung einer komplexen Zahl (complex number) mittels I:
> z := x + I*y;
Spezielles Beispiel:
> a := 2 + 3*I;
Realteil (real part) von a:
> Re(a);
Imaginärteil (imaginary part) von a:
> Im(a);
Betrag (absolute value) von a:
> abs(a);
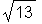
> conjugate(a);
Phasenwinkel (principal value of argument) :
> argument(a);

Normierung von a auf die Länge 1:
> signum(a);
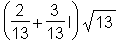
Polarschreibweise:
> convert(a, polar);
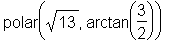
> polar(2, 3);
Komplexe Ausdrücke können Sie mit evalc kombiniert mit Re bzw. Im in ihre 'reellen' Bestandteile (also Real- und Imaginärteil) zerlegen. Dieses ist beispielsweise dann sinnvoll, wenn Sie umfangreiche ursprünglich komplexe Berechnungen durch reelle Fließkommaarithmetik beschleunigen möchten.
Ein Ausdruck, der mit evalc ausgewertet werden soll, darf nur komplexe Zahlen der Form 'z=x+I*y' beinhalten.
> restart: > z := x+I*y;
> c := a+I*b;
Aus diesen komplexen Zahlen besteht die Formel
> formula := z^2+c;
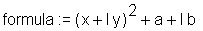
Die reellen Entsprechungen dieser Formel werden ermittelt:
> reell := evalc((Re(formula)));
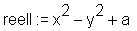
> imag := evalc((Im(formula)));
MAPLE EINFÜHRUNG - MPLINTRO 04.00a vom 14. Dezember 1998
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/m4.htm